重新认识红黑树

几年前笔者刚开始找实习时，曾经面过四次阿里的一面，几乎每个面试官都会问这样一个问题，如何在一亿条数据中快速查找到某条数据？笔者当时并没有回答上来，反而觉得客户端没有处理这么多数据的场景。不过现在回想起来，一种可行的方案就是红黑树了。

我们都知道红黑树既是二叉搜索树又是平衡二叉树，最坏情况下的时间复杂度为 $2\log_{2}N$，所以当 $N=100000000$ 时至多需要大约 44 次查找即可。红黑树之所以如此高效，是因为 其定义 保证了它在最坏情况下也基本是自平衡的：

1. 结点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色，注意叶子是 NIL 结点。
4. 每个红色结点必须有两个黑色的子结点，即从每个叶子到根的所有路径上不能有两个连续的红色结点。
5. 从任一结点到其每个叶子的所有 简单路径 都包含相同数目的黑色结点。

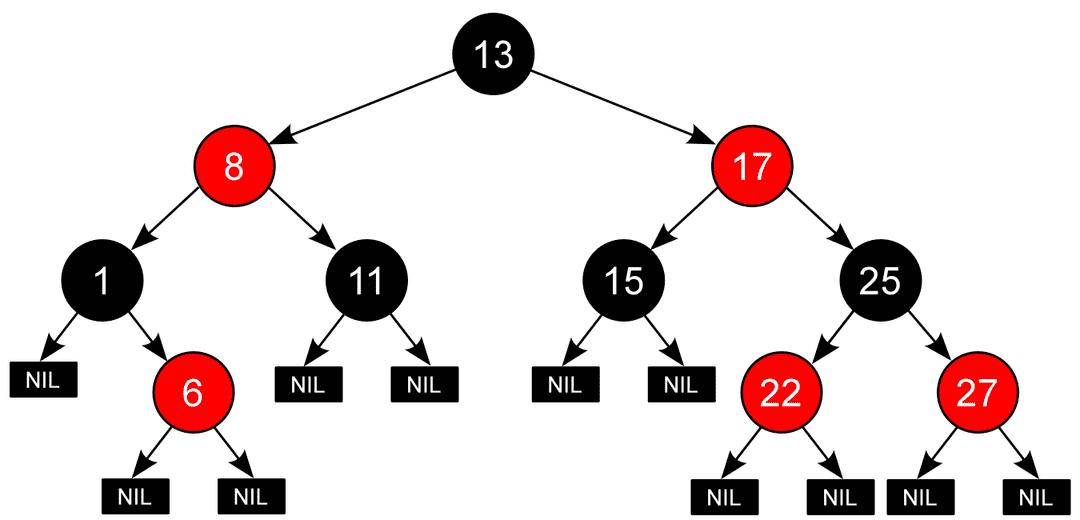
这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。

要知道为什么这些性质确保了这个结果，注意到性质 4 导致了路径不能有两个毗连的红色结点就足够了。最短的可能路径都是黑色结点，最长的可能路径有交替的红色和黑色结点。因为根据性质 5 所有最长的路径都有相同数目的黑色结点，这就表明了没有路径能多于任何其他路径的两倍长。

不过以上都是老生常谈了，相信大多数博客也都是这么介绍的。但都没有回答一个关键的问题，即红黑树究竟是怎样诞生的？

我们一般都是通过观察结构特性来理解数据结构，但红黑树不一样的地方在于，它跳出了结构特性这种抽象的骨架，变得具体了 —— 加上了颜色，使得理解难度瞬间上升。读者可能明白红黑树是怎样运行的，但却不一定知道它是怎样诞生的，这就有点知其然不知其所以然了。

笔者最近重新翻阅了《算法（第 4 版）》，发现书中介绍了一种名为「2-3 平衡树」的数据结构，这种数据结构符合我们对数据结构的一贯认知 —— 没有任何颜色，并且与红黑树完美等价，非常容易理解。事实上该书的作者 Sedgewick 也是 1978 年红黑树诞生的论文的两名作者之一（嗯，果然还是作者本人的阐述比较透彻 🤔

若读者身边有吃灰的《算法（第 4 版）》，请直接查阅「3.3 平衡查找树」章节，不用继续往下读了；若读者对 2-3 平衡树与红黑树之间的转换已经有所了解，则也不用往下读了 —— 毕竟本文不过是书中内容的复述而已。那么接下来就让我们开始吧。

2-3 平衡树由两类结点组成：

• 2- 结点，该结点包含一个值和两个子结点，其左子结点的值小于它，而右子结点的值大于它。
• 3- 结点，该结点包含两个值和三个子结点，其左子结点的值小于它，其右子结点的值大于它，而中子结点的值位于该结点的两个值之间。

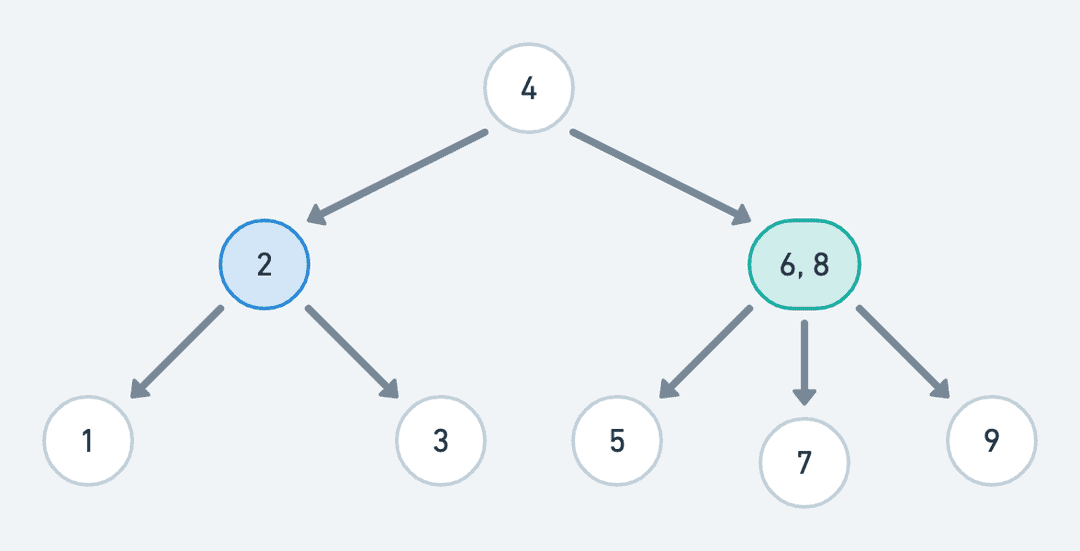
基于这两类结点的查找操作非常简单，几乎就和递归遍历二叉树一样。唯一不同的是，对于 3- 结点，需要多递归一次中间的子结点。我们可以用一段 Kotlin 代码简单表示这段逻辑：

// 如果是 2- 结点，则 min = max 且 middle = null
class TreeNode(var min: Int, var max: Int) {
    var left:   TreeNode? = null
    var right:  TreeNode? = null
    var middle: TreeNode? = null
}

// target 为我们希望查找的值，如果找到了则返回 true，否则返回 false
fun dfs(root: TreeNode?, target: Int): Boolean {
    if (root == null) return false
    if (target == root.min || target == root.max) return true
    if (target < root.min) return dfs(root.left, target)
    if (target > root.max) return dfs(root.right, target)
    // root.min < target && target < root.max
    return dfs(root.middle, target)
}

关键点在于构造 2-3 平衡树的过程，读者应当会好奇 3- 结点是如何被构造出来的。同时我们也将看到，如果按照此方法构造一棵树，那么这棵树基本是自平衡的。

以 4 → 2 → 1 → 3 的顺序插入结点，我们可以很轻易地构造出上图左边的 2- 结点分支。接着按照 6 → 5 → 7 → 8 → 9 的顺序插入结点，上图右边的 3- 结点分支构造过程如下：

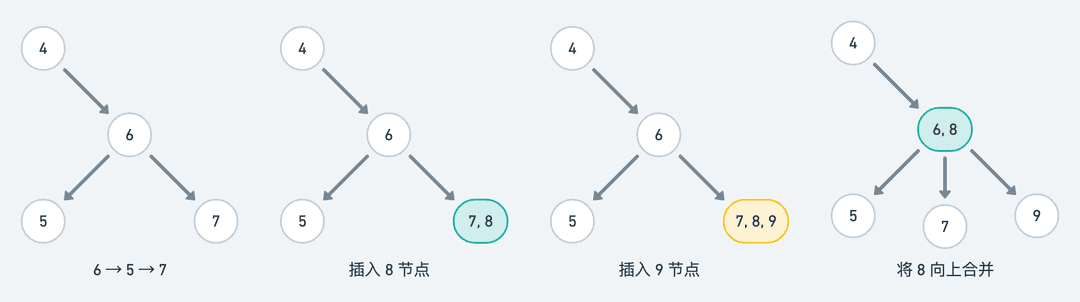
1. 当插入 8 结点时，我们将其与 7 结点合并成为一个 3- 结点 (7, 8)，而不是将其作为 7 结点的子结点，这样就能保证整棵树仍然是自平衡的。
2. 当插入 9 结点时，我们将其与 (7, 8) 结点合并成为一个 4- 结点 (7, 8, 9)；接着将 (7, 8, 9) 结点的中间值 8 提取出来，向上合并到 6 结点使之成为一个新的 3- 结点 (6, 8)；而 7 结点成为 (6, 8) 结点的中子结点，9 结点成为 (6, 8) 结点的右子结点；此时整棵树仍然是自平衡的。

我们继续按照 10 → 11 的顺序插入结点，看看会发生什么：

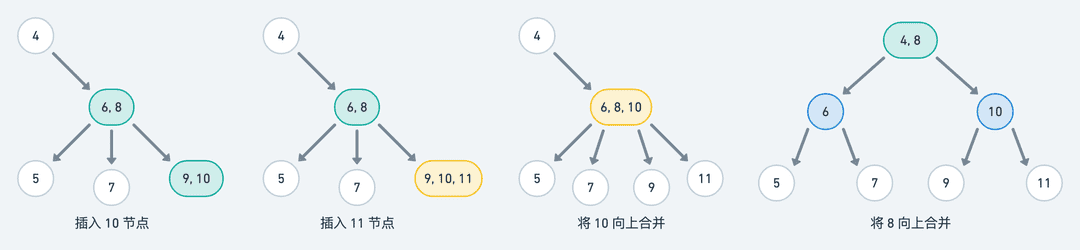
1. 当插入 10 结点时，我们将其与 9 结点合并成为一个 3- 结点 (9, 10)。
2. 当插入 11 结点时，我们将其与 (9, 10) 结点合并成为一个 4- 结点 (9, 10, 11)；接着将 (9, 10, 11) 结点的中间值 10 提取出来，向上合并到 (6, 8) 结点使之成为一个新的 4- 结点 (6, 8, 10)；而 9 结点成为 (6, 8, 10) 结点的偏右结点，11 结点成为 (6, 8, 10) 结点的右结点。
3. 由于 (6, 8, 10) 结点仍然是一个 4- 结点，我们需要将其中间值 8 提取出来，继续向上合并到 4 结点使之成为一个新的 3- 结点 (4, 8)；剩下的 (6, 10) 结点有两个值和四个子结点，我们需要将其分裂成 6 结点和 10 结点，从而满足 2- 结点的结构。

读者应该不难想象，此时整棵 2-3 树仍然是自平衡的。更复杂的场景这里就不继续列举了。如果按照上述顺序构造一棵普通的的二叉查找树，则是不平衡的（右偏）。

但构造一棵 2-3 平衡树的成本远比构造一棵普通的二叉查找树要高得多，我们还是希望构造过程相对简单。解决方案是把 3- 结点分裂为两个 2- 结点：

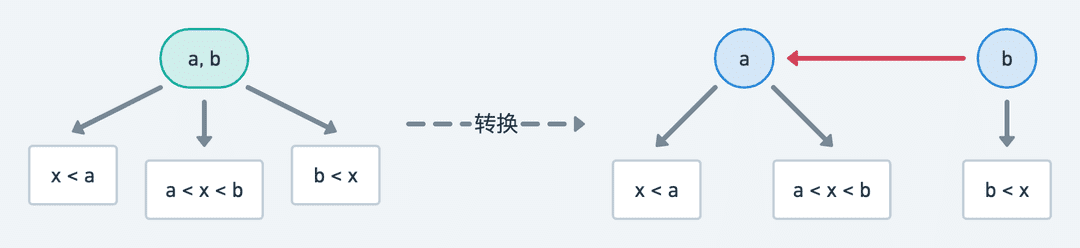
我们只需要将 3- 结点分裂出的两个 2- 结点之间的链接标记为红色，其余正常的 2- 结点之间的链接都标记为黑色，是不是瞬间就有内味了？维基百科是将结点定义为红色或者黑色，而我们是将结点之间的链接定义为红色或者黑色，事实上这是红黑树的一种等价定义：

1. 红链接均为左链接。
2. 没有任何一个结点同时和两条红链接相连。
3. 叶子结点 (NIL) 到根结点的路径上的黑链接数相同，即完美黑色平衡。

满足上述三点的含有红黑链接的二叉查找树即是红黑树。相对与 2-3 平衡树而言，我们稍微损失了一点平衡性（将 3- 节点分裂为两个 2- 节点），但换取到了构造过程的便利性。

现在我们已经大概了解红黑树的来源了。至于如何构造一棵红黑树（左旋、右旋、颜色转换）则超出了本文的范围，感兴趣的读者可以自行研究。最后为什么是红黑树，不是绿黑树、黄蓝树？看看 Sedgewick 自己怎么说：

A lot of people ask why did we use the name red–black. Well, we invented this data structure, this way of looking at balanced trees, at Xerox PARC which was the home of the personal computer and many other innovations that we live with today entering[sic] graphic user interfaces, ethernet and object-oriented programmings[sic] and many other things. But one of the things that was invented there was laser printing and we were very excited to have nearby color laser printer that could print things out in color and out of the colors the red looked the best. So, that’s why we picked the color red to distinguish red links, the types of links, in three nodes. So, that’s an answer to the question for people that have been asking.